Wie von selbst: Echtzeit Optimierung mit Banditen
Alle reden vom selbstfahrenden Auto.
Wir sprechen heute über das automatisierte Marketing.
Wohin die Reise geht
Vielfach konkurrieren um wertvolle Marketingslots unterschiedliche Varianten eines Themas. Welche aber ist die beste Variante?
Genauso, wie das selbstfahrende Auto ein Ziel benötigt, um durch den Straßendschungel zu navigieren, benötigt man auch Ziele bei der Echtzeit-Optimierung des auszuspielenden Shop-Contents. Click-Through-Rate (CTR) und Conversion-Rate (CVR) sind die klassischen Metriken, um den Erfolg einer Marketingmaßnahme zu messen. Das ändert sich nicht bei der Echtzeit-Optimierung.
In der Echtzeit-Optimierung ändert sich jedoch zur Laufzeit die Häufigkeit, mit der eine Variante gespielt wird. Diese Idee hat ihren Ursprung in der Untersuchung von Glückspielen: habe ich mehrere Einarmige Banditen, die unterschiedliche, zunächst unbekannte Gewinnwahrscheinlichkeiten haben, kann ich durch Probieren der Arme des Banditen versuchen, die Gewinnwahrscheinlichkeit zu ermitteln. Sofern ich einen Trend erkenne, ziehe ich einfach häufiger am Arm des Banditen, der den meisten Gewinn verspricht. In unserem Fall ist das Glücksspiel die unbekannte Reaktion der User auf die Einblendung einer Marketingmaßnahme.
Naiv würde man also vielleicht so vorgehen: teste einfach alle Varianten gegeneinander und sorge dafür, dass die meiste Zeit die beste Variante zu sehen ist. Darin steckt aber auch das Dilemma der Echtzeit-Optimierung.
Exploration und Exploitation
Befinde ich mich im Test - also in der Exploration - zeige ich womöglich auch Varianten, die nicht so gut funktionieren, und ich verliere mit jeder Einblendung einer schlechten Variante Conversion. Zeige ich die gerade beste Variante - bin also in der Exploitation - verpasse ich womöglich die Chance, dass eine andere Variante doch noch vorbeiziehen könnte. Insbesondere dann, wenn "die beste Variante" gar nicht so fix ist, sondern abhängig von externen Einflüssen mal so, und mal so sein kann.
Der ungewöhnlich und spontan verlängerte Sommer 2016 korrespondierte beispielsweise nicht mit den Herbst-Themes zahlreicher Modeshops. Wer Fernsehwerbung schaltet, muss sich auf einen Ansturm bestimmter Zielgruppen gefasst machen, deren Interessensschwerpunkt womöglich ganz woanders liegt als jener der Besucher des üblichen Tagesverlaufes. Man sieht schon: die beste Variante ist eingebettet in eine Umgebung, die sich über die Zeit verändert. Der Rising Star wird zum Fallen Angel - oder umgekehrt.
Im Marketing würde man Exploration vielleicht vergleichen können mit einem Invest in die Diversifikation, und die Exploitation wäre der Return durch eine Konzentration auf das Wesentliche.
Die naive Strategie
Nun aber braucht es eine Strategie, um Varianten gegeneinander zu testen - und zwar gerade so oft, wie notwendig, um die beste Option möglichst oft ausnutzen zu können.
Sagen wir mal, die Besucher werden in zwei Gruppen aufgeteilt. 10% der Benutzer sehen eine zufällig gezogene Variante. 90% der Benutzer sehen die aktuell beste Variante. Jedes Mal, wenn ein Versuch ein gewünschtes Verhalten beim Benutzer erzeugt hat (im einfachsten Fall: ein Klick auf den Call-to-Action-Button), melde ich meiner Variante eine Belohnung zurück (engl. Reward).
Der Mathematiker würde sagen, die 10%-Größe ist ein Parameter - und den nennen wir mal epsilon. Mit einer Wahrscheinlichkeit von epsilon befinde ich mich in der Explorationsgruppe, und mit der Gegenwahrscheinlichkeit 1-epsilon in der Exploitationsgruppe:
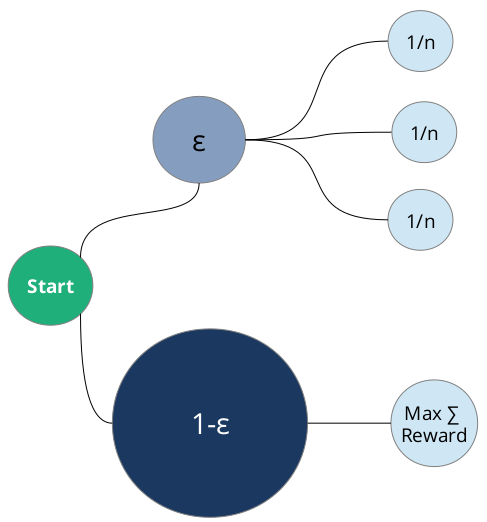
In der Exploitationsgruppe (1-epsilon) wird schlicht die Variante gezeigt, die den meisten Reward geerntet hat - bezogen auf die Einblendungen, die diese Variante erfahren hat. Die Explorationsgruppe (epsilon) hingegen zeigt alle verfügbaren Varianten mit einer gleichverteilten Wahrscheinlichkeit an.
Konvergenz zum Optimum
Herzlichen Glückwunsch, wenn Sie bis hier hin gekommen sind - das war das ganze Geheimnis des epsilon-Greedy-Algorithmus, der einfachste Algorithmus zur Echtzeit-Optimierung: Am häufigsten spielen wir die beste Variante, aber wir lassen die Türen offen, um andere Varianten im Feld zu testen. Im direkten Vergleich zu einer rein zufälligen Ausspielung der Varianten (typischer A/B-Test oder rein randomisierter Algorithmus) zahlt die epsilon-Greedy-Strategie positiv auf die Conversion ein:
Angenommen, man testet zwei Varianten, die da heißen A und B. Wir wissen noch nicht, was die tatsächliche Conversion-Rate ist, aber in unserer Simulation setzen wir die Varianten mal auf 0.1 bzw. 0.3
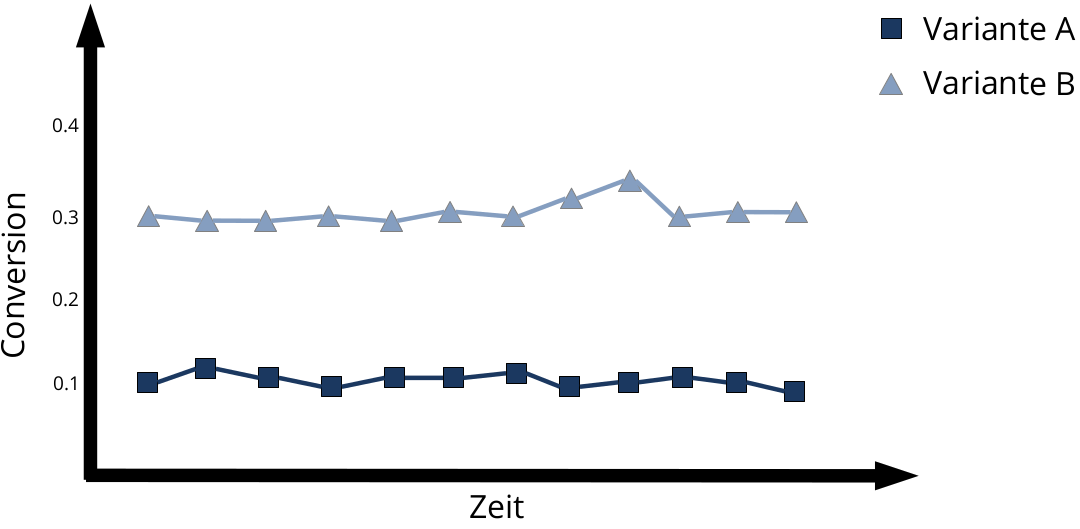
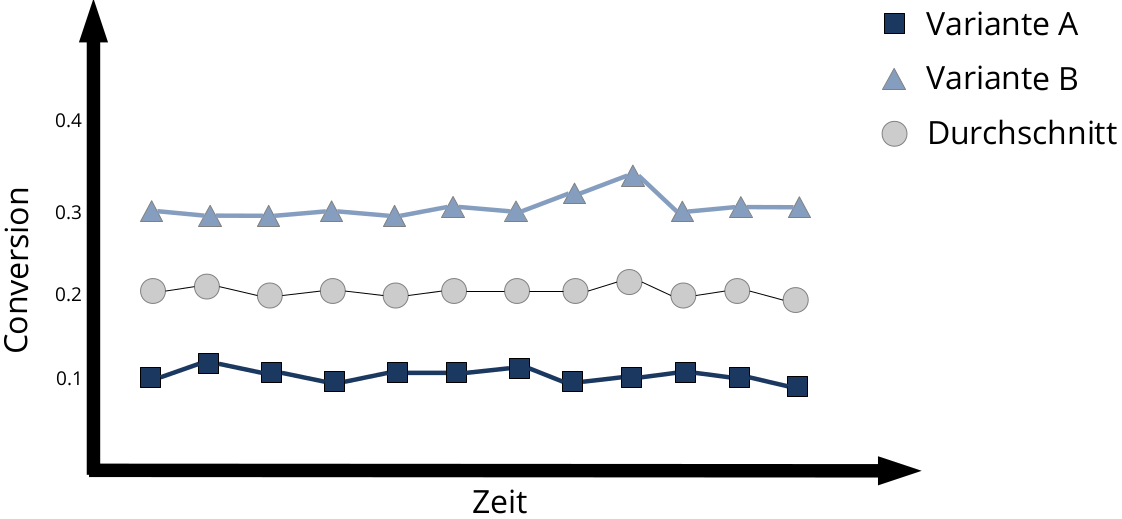
Würden sich beide Varianten einfach abwechselnd zeigen (mit einer 50:50 Chance), erreicht man gemittelt über alle Varianten natürlich nur eine durchschnittliche CVR:
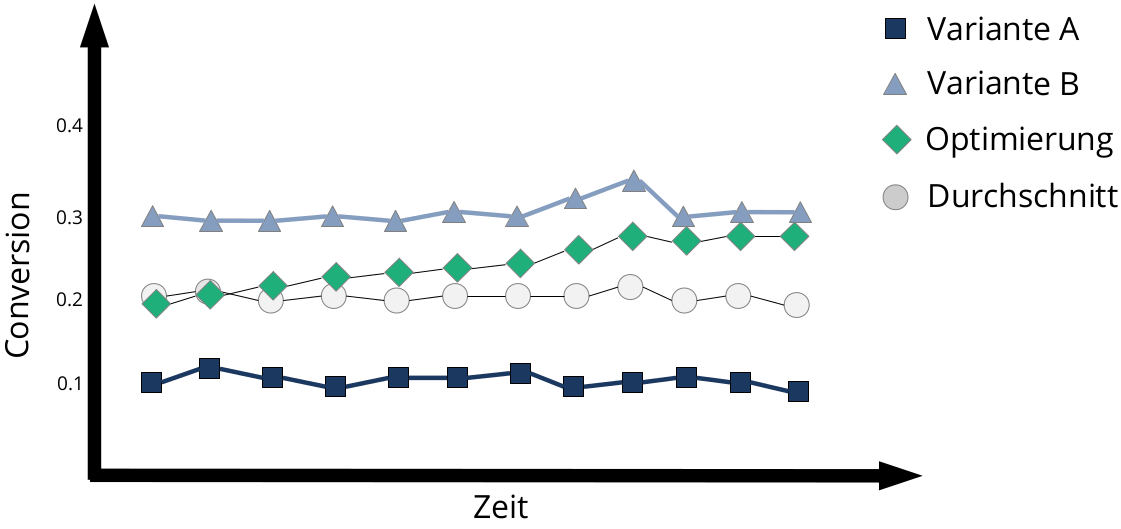
Setzen wir jedoch eine Optimierungsstrategie an, nähert sich die effektive Conversion-Rate über die Zeit der bestmöglichen Conversion Rate an - der Algorithmus konvergiert:
Vom Urtyp zum verfeinerten Algorithmus
epsilon-Greedy ist intuitiv einfach und effektiv, so dass man damit prima starten kann. Den Zufall schlagen wir mit diesem Vorgehen allemal.
Alle anderen Algorithmen sind letzlich nur eine Verfeinerung dessen, was epsilon-Greedy schon leistet. Eine erste Verfeinerung wäre es beispielsweise, den Wert für epsilon am Anfang unseres Experimentes groß zu setzen, um zunächst möglichst viel Information über die Varianten zu sammeln, und über die Zeit den Explorationsparameter epsilon asymptotisch kleiner werden zu lassen. In der Tat hat diese erste Optimierung der Optimierung auch einen Namen, nämlich annealing epsilon-Greedy (annealing ist engl. und bedeutet Abkühlung: ich fange also mit großer Wärme und Unordnung an, und kühle bis zur Stabilität ab).
Im Konfidenzintervall bleiben - UCB
Eine etwas andere Strategie implementiert der UCB-Algorithmus.
Das Akronym steht für Upper Confidence Bound (obere Konfidenzschranke). Durch Ausnutzung einer statistischen Ungleichung von Chernoff-Hoeffding wird das Verhältnis von Exploration und Exploitation dergestalt austariert, dass der Informationsgehalt bei jeder Variante so gesättigt sein muss, dass die Annahme über die Performance eine Variante innerhalb eines Konfidenzintervalles liegt.
Im Grunde ist die Ermittlung der "besten Variante" ja eine statistische Erhebung. Wir glauben, dass Variante B besser ist als Variante A, weil wir in Stichproben messen, wie gut die Varianten funktionieren. Mit Hilfe der Ungleichung von Chernoff-Hoeffding kann der benötigte Stichprobenumfang abgeschätzt werden, so dass Aussagen getroffen werden, die innerhalb eines statistischen Konfidenzintervalles liegen.
Intuitiv könnte man sagen, dass der Algorithmus neugierig bleibt: immer, wenn ein Konfidenzbereich verlassen wird, sammelt UCB neue Information und geht über in die Exploration. Sind genug Informationen gesammelt, schaltet der Bandit wieder auf Exploitation. Dadurch ergibt sich ein Zickzack-förmiger Wechsel zwischen Exploration und Exploitation, im Gegensatz zum epsilon-Greedy, bei dem die Explorationsgröße epsilon unabhängig von den gesammelten Informationen gesetzt wird.
Bayesian Bandits - Lernen aus Evidenz
Eine weitere Klasse von Algorithmen basiert auf der Statistik vom guten, alten Bayes.
Von Bayes haben wir gelernt, dass wir eine subjektive Annahme (ein Glauben) im Lichte neu gesehener Daten an die Wirklichkeit anpassen können. Aus einer a priori Annahme (der uninformierte Glaube zum Startzeitpunkt) wird so eine posterior Annahme (der gefestigte Glaube, nachdem die evidenten Daten gesehen wurden). Lange Zeit herrschte leidenschaftliche Aufregung in der Welt der Statistiker, es gab regelrechte Grabenkämpfe zwischen den Frequentisten, den Objektivisten und den Bayesianern.
Heutzutage hat sich die Bayesianische Statistik im Umfeld des maschinellen Lernens fest etabliert: Jedes Mal, wenn wir neue Daten sehen, können wir daraus lernen. Das passt natürlich hervorragend zum bayesianischen Update-Schritt. Mit jedem Update-Schritt steigt die Kredibilität der Annahmen.
Wenn wir wenige Daten (also wenig Evidenz) haben, ist unser Glaube folgerichtig noch nicht so gefestigt: wir nehmen an, dass die reale Performance einer Variante vielleicht bei einer CVR von 8.9% liegen könnte, +/- 4% - also irgendwo zwischen 4.9% und 12.9%, wobei wir den Schwerpunkt der Verteilung bei 8.9% am wahrscheinlichsten annehmen. Je mehr Daten wir sammeln, desto schmaler können wir das Plus-Minus-Band um unseren Glauben ziehen.
Wenn wir auf einer Bernoulli-Reise mit 0=kein Erfolg und 1=es gab einen Erfolg sind, bietet sich im Kontext der bayesianischen Statistik die Betaverteilung an:
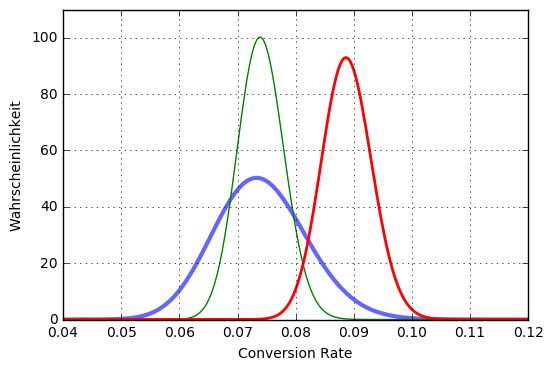
Wenn wir wie im obigen Bild drei Varianten haben, deren CVR wir jeweils mit einer Beta-Verteilung schätzen, sehen wir, dass die rote Variante offenbar auf der Conversion-Achse der Winner ist. Nichtsdestotrotz überlappt sich die Verteilung der roten Variante mit den Verteilungen der blauen und grünen Variante. Ziehen wir nun aus jeder Verteilung eine Zufallszahl, so ist die Chance, dass die größte Zufallszahl zur roten Variante gehört, sehr groß: wir exploiten. Es gibt aber auch eine stochastische Chance, dass die größte gezogene Zahl aus der blauen oder grünen Variante stammt: wir explorieren.
Am stärksten überlappt die rote Verteilung mit der blauen Verteilung, was vor allen Dingen daran liegt, dass die blaue Verteilung nicht so spitz ist wie die beiden anderen: dieses breite Auslaufen bedeutet, dass wir noch nicht sehr viele Informationen über die blaue Variante gesammelt haben. Die Exploration bevorzugt also die Varianten, die wir noch nicht häufig genug getestet haben. Ganz natürlich, ganz stochastisch, einfach nur durch das Ziehen von Zufallszahlen.
Und welches Banditerl hätten wir nun gerne?
Wenn epsilon-Greedy in der Regel besser funktioniert als der Zufall, so arbeitet UCB in der Regel noch ein bisschen besser als epsilon-Greedy und der Bayesian Bandit arbeitet noch ein bisschen besser als der UCB.
So einfach ist die Aussage in der Wirklichkeit natürlich nicht zu treffen, da alle Algorithmen Vor- und Nachteile haben - hinsichtlich Lerngeschwindigkeit, Überanpassung, der Fähigkeit, auf Schwankungen zu reagieren sowie dem tatsächlichen Ausspielungsverhalten - also wann und wie oft hintereinander welche Variante gezeigt wird.
Eine besondere Geschmeidigkeit im Real-World-Betrieb ist beim Bayesian Bandit zu erwarten, insbesondere beim kalten Start: durch das Sampling ist die Informationsbeschaffung stochastisch fair verteilt, und die Exploitation stellt sich gleichermaßen automatisch ein. Da sich im Laufe der Zeit eine Sättigung einstellen kann (wenn die Varianzen der posterior Beta-Verteilungen schmaler und schmaler werden), würde auch die Explorationsleistung zunehmend kleiner werden. Will man schnell lernen und zum Optimum konvergieren, ist das ganz hervorragend; will man Trendwechsel auch nach einigen Tagen noch schnell erspüren, ist das eher schlecht. Sofern man sich dessen bewusst ist, kann man dem über mathematisches Atmenlassen und Kombinieren entgegenwirken.
Neben den beschriebenen Algorithmen in Reinkultur gibt es natürlich auch noch jede Menge mehr in der Welt der Banditen zu entdecken.
Fortsetzung folgt
Bildnachweise
"3D Bullseye", Lizenz: Creative Commons Attribution 2.0 Generic, Autor: ccpixs.com


